Saltar al contenido
Noticias

¿Qué es Hexadecimal?

por Yendry Lopez Gomez
Sistema hexadecimal

Un sistema numérico puede ser definido como un conjunto de reglas aplicadas sobre una serie de símbolos para así construir todos los números válidos del sistema. Las reglas definidas son inherentes a cada sistema de numeración. No obstante, todos deben cumplir el principio de que para representar los número válidos del sistema solo se pueden utilizar los símbolos definidos por el sistema.

En informática se emplea el sistema binario, el cual solo usa los símbolos 0 y 1. Cada uno de estos representa un estado traducido a impulsos eléctricos por los componentes del ordenador. No obstante, es posible siempre representar un determinado valor en cualesquiera de los sistemas numéricos. Es decir, podemos convertir un número en cualquier sistema, hacia otro sistema numérico.

Dentro de los sistemas de numeración tenemos el sistema hexadecimal el cual es también usado en los sistemas informáticos.En el siguiente artículo te explicamos en qué consiste el sistema hexadecimal y lo métodos de conversión a otros sistemas de numeración. Te invito a que continúes leyendo, ya comenzamos.

Tabla de contenidos

Definición de hexadecimal

Hexadecimal significa que es en base a 16. Para que entiendan un poco mejor haremos una analogía referente al sistema decimal, que es el comúnmente utilizado. En el sistema decimal, lo números se construye en base de diez. El conjunto de símbolos empleados en el sistema decimal, son las cifras numéricas del 0 al 9. Con estos diez símbolos podemos representar cualquier número del sistema.

El sistema hexadecimal es un sistema posicional, donde el valor del número depende de la posición que ocupa cada dígito dentro de la representación del número. Siendo así, que el valor 5 este en la posición uno tiene un valor distinto si está en la posición 3 del número.

Pues el sistema hexadecimal tiene su base construida sobre 16. Consta de dieciséis símbolos posibles para crear cualquier número, estos son:

Símbolos del sistema hexadecimal.
Conjunto de símbolos hexadecimales.

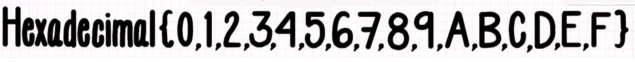
Los símbolos representados por las letras corresponden a los valores en sistema decimal 10,11,12,13,14,15. Es posible usar letras minúsculas en la notación empleada para representar el sistema hexadecimal, en lugar de mayúsculas.

Representación de un número hexadecimal

Para representar un número en el sistema hexadecimal, cada dígito es colocado en una posición específica del número, siendo multiplicado por la base del sistema, en este caso 16. Veamos en la práctica cómo convertir un número hexadecimal al sistema decimal, que es el más usado en la vida cotidiana. Supongamos que tenemos el número hexadecimal 4A01B,

Pues para convertirlo solo tenemos que sumar cada uno de sus dígitos multiplicado por la base 16 elevado a la posición, contadas de derecha a izquierda comenzando por la posición 0, que ocupa el dígito. En este caso hemos usado el símbolo ^ para representar la potencia.

4A01B= 4×16^4 + Ax16^3 + 0x16^2 + 1×16^1 + Bx16^0

Reemplazando las operaciones de multiplicación y suma decimales tenemos que:

4A01B= 262 144 + 40 960 + 0 + 16 + 11

Realizando la suma obtenemos el resultado final de

4A01B= 303 131.

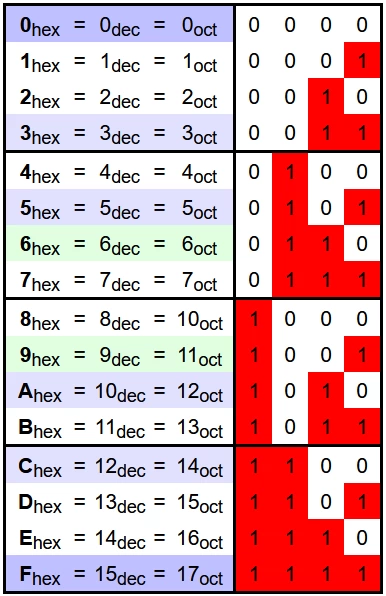
Valores en los sistemas hexadecimal, decimal, octal y binario

Como ya planteamos anteriormente, cualquier número en un sistema dado, puede ser llevado hacia otro sistema. En la siguiente imagen podemos ver los valores y su correspondencia entre los sistemas de numeración hexadecimal, decimal, octal y binario.

Relacion entre los valores de sistema hexadecimal, decimal. octal y binario.
Correspondencia entre los sistemas hexadecimal, decimal, octal y binario

Operaciones aritméticas

Con el sistema hexadecimal es posible realizar las operaciones aritméticas básicas de suma y resta. A continuación, realizamos una explicación de cómo proceder en cada operación.

Suma

Para realizar la suma de números hexadecimales, tenemos que extrapolar al sistema decimal. La suma de cada dígito se realiza pensado en una suma decimal.

Por ejemplo, si queremos sumar 6+3 en hexadecimal lo sumamos como si fuera decimal, en este caso obtendremos 9. Ahora bien, en el resultado es dónde está el quid de la cuestión. Para poder representar el resultado en valor hexadecimal, tenemos que comprobar que el dígito que dio como resultado sea un símbolo hexadecimal. En este caso el 9 lo es, por tanto, el resultado se queda como esta.

Vemos otro ejemplo, si queremos sumar 9 + D. En este caso D corresponde al número decimal 13. Entonces la suma la realizaremos sumando 9 + 13, obteniendo el número decimal 22. En este caso, el número 22 no es un símbolo del sistema hexadecimal, por tanto, tenemos que representarlo en dicho sistema.

Para hacer esta operación tenemos que realizar restas consecutivas de 16 al resultado hasta que lleguemos un valor que sí pertenezca al conjunto. En este caso haríamos 22-16=6. Aquí ya paramos de restar porque 6 si es un valor hexadecimal.

Este valor 6 será el primer valor del resultado de derecha a izquierda. Para completar, contamos cuántas veces restamos 16 y se usa este valor como acarreo positivo en la columna anterior a la suma. Como aquí no hay ningún valor, puse se quedará como 1. Entonces el resultado de sumar 9+13=16. Tenga en cuenta que este número no se lee como dieciséis, sino como uno seis.

Suma hexadecimal .
Suma hexadecimal.

Resta

El proceso de resta puede resultar algo engorroso, ya que hay varias reglas que cumplir. En primer lugar, debemos analizar si el minuendo es mayor o menor que el sustraendo. La mejor manera de analizar esto es mediante ejemplos.

Supongamos que queremos restar 6A – 2. De manera análoga a la suma, tenemos que pensar la resta de dígitos en base decimal. En este caso restamos 10 que es A en hexadecimal a 2 obteniendo 8, que será el primer dígito. Después restamos 6 a nada y obtendremos 6.

Resta de números hexadecimales.
Resta hexadecimal.

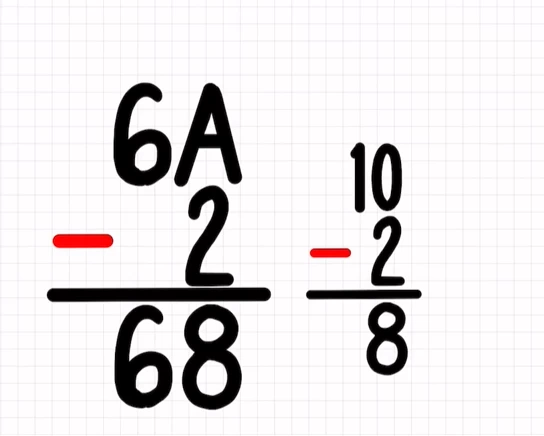
Vemos otro ejemplo, si queremos restar 3A1 – F0 procedemos al igual que en la resta decimal, de derecha a izquierda digito a digito. En primer lugar, restamos 1 – 0 obteniendo 0. A continuación debemos restar A-F. A representa el número decimal 10 y F al 15.

Pues en este caso tenemos que el minuendo es menor que el sustraendo. Cuando esto ocurre tenemos que pedir una unidad prestada al siguiente dígito. Pero la cuestión es que, en resta hexadecimal, cada unidad pedida representa en realidad 16 unidades, por tanto, ese es el valor que sumamos al minuendo.

En este caso, A+16=10+16=26. A continuación procedemos con la resta, restando F (15) a 26 para obtener 11. Y el once se representa en hexadecimal como B.

Continuamos con la resta ahora del próximo dígito, que es 3. Pero, como se le había pedido una unidad, tenemos 2 – nada que es 2.

Por tanto, restar 3A1 – F0 =2B1

Resta hexadecimal.
Resta hexadecimal.

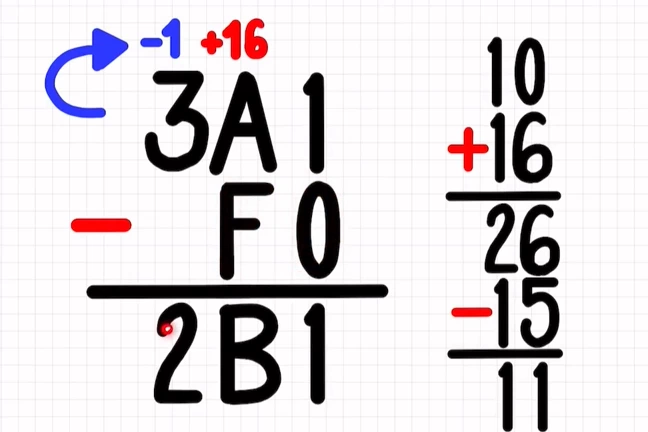
Uso del sistema hexadecimal en la computación

En los sistemas computarizados fue introducido el sistema hexadecimal en el año 1963 por la empresa IBM. Este sistema este ampliamente ligado a las operaciones que realiza la CPU de un ordenador.

Las operaciones computadas por el CPU utiliza el byte como la unidad básica de memoria. Ahora bien, un byte no es más que la unión de 8 bits, por tanto, un byte puede representar un número máximo de 2^8 posibles valores.

Aritméticamente, 2^8 pude ser representado como 2^4 x 2^4, que es lo mismo que decir 16×16, donde en sistema hexadecimal es 1×16^2 + 0x16^1 + 0x16^0. Esto equivale al número hexadecimal 100. En conclusión, un byte se corresponde exactamente con dos dígitos hexadecimales.

Artículos relacionados que te podrían resultar interesantes:

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *